- Dissertations on Machine Learning, “Stacking” and “Voting”
- Machine Learning – AutoML vs Hyperparameter Tuning
- Precise information filtering deriving from laws present in nature
- Timeseries Forecast
- Protetto: What’s the frequency Kenneth
When the probability of measuring a particular value of some quantity varies inversely as a power of that value, the quantity is said to follow a power law, also known variously as Zipf’s law or the Pareto distribution (1). Looking at the figures, it’s really astonishing how most of the information is carried by such a low pecentage of words in a text.
Having in mind other objectives, C. Shannon dedicated most of his life and research to pieces of work that became fundamental for the Information Theory, and the final results allow to understand what is the acceptable loss of information in order to transfer a sequence of signals in an efficient way.
We have transposed the two approaches in order to perform a deterministic research in text by filtering the total words in a number of texts of the same kind by identifying the keywords of an ontological map built for the purpose.
We allowed the human to perform reinforcement learning on the submitted text and after a very low number of iterations we got incredible results.
In about 88% of cases it was possible to identify exactly the piece of information we were looking for and in all cases we were able to identify the two or three sentences that contained the information, out of documents exceeding the 130 pages in length.
This approach, being a “weak AI” achievement, exploits the following advantages:
- it uses certain, trackable and validated data sources;
- it obtains certain results, not probabilistic, not using generative AI;
- it relies on the ability of the domain expert for reinforcement learning;
- the knowledge base can be kept in-house and will represent a corporate asset.
(to be continued)
By A. Ballarin, G.Fruscio
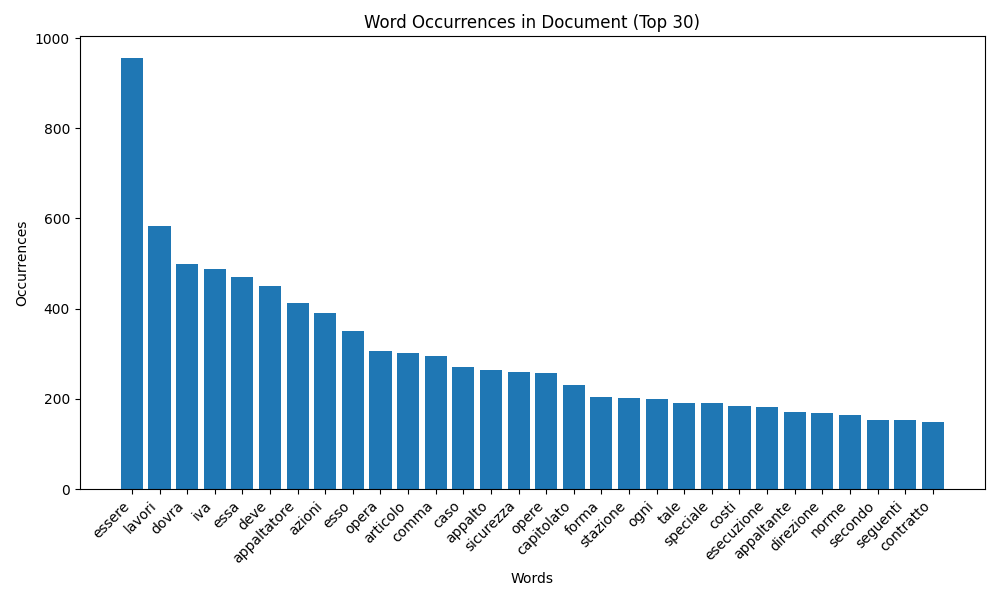
The Zipf-Mandelbrot-Pareto law is a combination of the Zipf, Pareto, and Mandelbrot distributions. It is a power-law distribution on ranked data that is used to model phenomena where a few events or entities are much more common than others. The probability mass function of the Zipf-Mandelbrot-Pareto law is given by a power-law distribution on ranked data, similar to Zipf’s law. The Zipf-Mandelbrot-Pareto model is often used to model co-authorship popularity, insurance frequency, vocabulary growth, and other phenomena (2,3,4,5)
Applications of the Zipf-Mandelbrot-Pareto law include modeling the frequency of words in a corpus of text data, modeling income or wealth distributions, and modeling insurance frequency. The Zipf-Mandelbrot-Pareto law is also used in the study of vocabulary growth and the relationship between the Heaps and Zipf Laws (2,3,4,5)
Overall, the Zipf-Mandelbrot-Pareto law is a useful tool for modeling phenomena where a few events or entities are much more common than others. It has applications in linguistics, economics, insurance, and other fields (2,3,4,5)
- http://www.cs.cornell.edu/courses/cs6241/2019sp/readings/Newman-2005-distributions.pdf
- https://eforum.casact.org/article/38501-modeling-insurance-frequency-with-the-zipf-mandelbrot-distribution
- https://www.r-bloggers.com/2011/10/the-zipf-and-zipf-mandelbrot-distributions/
- https://journalofinequalitiesandapplications.springeropen.com/articles/10.1186/s13660-018-1625-y
- https://www.sciencedirect.com/science/article/pii/S0378437122008172

